非線形システム概論 ─ Yet Frequently Asked Questions─

$Lastupdate: Mon Oct 31 11:33:32 2005 $

4/12 / 4/19 / 4/26
5/10 / 5/17 / 5/24 / 5/31
6/7 / 6/14 / 6/21 / 6/28
7/5 / 7/12 / 7/19 / 7/26

4月12日
- 「シラバスに書いた」とおっしゃっていましたが，今年はシラバスをもらっていないと思います．今年のシラバスはあるのですか？
- 今年からオンラインになりました．埼玉大学のホームページから辿ってください．
- 出席点についてですが，どのくらいの厳しさで採点するのでしょうか？ある程度の内容があれば満点をくれるのですか？
- 現在のところ，無意味でない内容を記述していたら，満点を与えるつもりです．但し，代理での記述，氏名だけの記述などの場合は， 0点にします．
- 毎回スライドをプリントで配っていただけるか， Webからダウンロードできるようして頂けると助かります．
- 既に第一回目に用いたスライドについても，少なくともWebからダウンロードするできるようにはしています．また，必要であれば，コピーを配布します．
- 日本語の参考書はないんですか?
- 第2回目の講義で紹介します．の予定でしたが，時間がなくなったので，ここでいくつか紹介します．徐々に増やしていく予定です．
  - 合原一幸著，カオス - 全く新しい創造の波，講談社,1993
  - イアンスチュアート著，須田不二夫・三村和男訳，カオス的世界像，白揚社，1992
  - 山口昌哉著，カオスとフラクタル，講談社ブルーバックス，1986
  - 森肇著，カオス--流転する自然，岩波科学ライブラリー，1995
  - 戸田盛和著，カオス--混沌の中の法則，岩波書店，1991
- コメント用紙のホームページでの解答は (昨年度?は) 2〜3回しか更新されなかった気がするのが不安なのですが，今回は大丈夫ですか?
- 質問が出る度に更新しています．昨年度もそうしていしました．
- 数学系の英語の単語について調べられる方法を紹介してほしい．
- 第2回目の講義で説明します．
- 端末で行うときはどの様になるのかを教えて頂きたいです．
- 行っていないので，ハッキリとしたことは言えませんが，説明しながらプログラムを作るなどのスタイルになると思われます．
- 試験よりもレポートのほうが考える時間もあるので，うれしいです．レポートの場合，具体的にはどんな感じなのでしょうか．
- 仮にレポートにした場合は，課題を出題し，それを皆さんに解答してもらうことにします．但し，レポート用紙は，僕に直接提出してもらい，その場で口頭諮問を行います．

4月19日
- 線形な差分方程式の振る舞いを，なぜ周期的なものと一定のものを分けるのですか？
- 最終的な振る舞いが異なるからです．
- 線形な差分方程式の係数Rがさらにまたほかの何かのパラメータに依存するような関数は，線形なのか，非線形なのか疑問に思いました．
- をっ!鋭い!なかなか良い質問です．これについては，次回紹介します．
- 非線形をまだ理解できていないようです．
- 安心して下さい．講義では非線形の説明をまだしていませんから．
- ハエの個体数が，前年のハエの数のみに依存するというのは正しい前提でしょうか？
- またまた，鋭い質問! 今回は正しいとしましたが，実際には他にも様々な要因が考えられるでしょう．但し，この講義の今日の話では，このような仮定を導入しました．複雑な現象を解析していく上では，ある程度の簡略化はしばしば必要になります．但し，それも実際の現象とモデルとの一致具合いがどうか，ということも考える必要があります．
- ハエの個体数だったら，前年の個体数に依存するが，その個体数が（気象などから）何らかの影響を受けたりとかするのでは？
- これも鋭いですね．仰有る通りです．答えは，上の質問に対するものと同じです．
- 漸化式が未来予想に使えるのですね．
- はい，使えます．ところで，「予想」という用語は，通常学術的な意味では用いないので注意してください．僕は講義中に，「予測」という用語を用いました．
- 爆発的に増加している生物や，急激に減少している生物などは，線形のほうがよく表現できると思います．
- 鋭いですね〜〜．確かにその通りですが，果たして，爆発的な増加がいつまでも続くでしょうか．急激な減少も同様です．次回，議論しましょう!
- 「差分方程式」というものの定義がわからず，よくイメージできませんでした．
- そりゃ，遅刻してくるからですよ・・・とりあえず，高校数学で習った，漸化式をイメージしてください．
- 授業でやった非線形である差分方程式の扱い方のイメージがつかめません．
- 大丈夫! 授業では，まだ非線形な差分方程式の扱い方をやっていませんから．次回お話しします．
- 図式解法を用いて非線形な方程式を解く時，最初の図が描けないような気がします．
- 非線形な場合でも，一変数であれば，そんなに難しい f を扱わないので多分大丈夫です．でも，確かに図に描くのが難しい場合もあると思いますが・・・
- 生物の個体数は前年の個体数に依存するので，関数に表せるようだが，本当に表せるのか，とても不思議です．
- 鋭いですね．確かに，本当に関数に表せるかどうか不思議です．
- 線形はあまり使えない気がしてショックです．
- おっと．線形はあまり使えないということはありません．線形理論は必要なものです．でも，十分でないということを主張しました．
- 僕もハエの個体数の変化は非線形だと思います．線形であらわせるほど単純ではないと思います．
- いいですね〜．その通りだと思います．こんど一杯やりながら議論しましょう．
- N_{t+1}=RN{t}+a (a:定数) のような， y切片のあるものも線形な式といえるのでしょうか？
- これも良い質問．広義の意味で線形と捉えても良いです．アフィン変換と言われることもあります．
- スライドの下の方の字が人の頭でよく見えません．
- ごめんなさい．次回からは，なるべく上に移るようにしますが，貴女も出来たら教室の前の方にきたらどうでしょう?
- 白板からの光の反射が少しまぶしくてつらい．もう少し暗くして欲しい．プロジェクタの光で見えない．
- 了解です．次回からは，気をつけます．また，見えにくいときは，講義中でもどんどん言ってください．
- 演習をやる時間が少し短かった．
- 今日はそうでしたね．次回からは増やすことにしたいと思います．
- 授業のペースはちょうどいいのですが，しゃべりが少だけ速い気がします．
- 申し訳ありません．今日はゆっくり話したつもりでしたが．次回から，聞き取りにくいところがあったら，すぐに言ってください．

4月26日
- ロジスティック写像で， R=4のときに， x_{t+1}=R(1-x_{t})x(t) は二度と同じ値を出さないと言いましたが， x_{0}=0.5となった後，1，0となって，その後 0 しか出てこないと思いますが，そうではないのですか？
- 確かに初期値を 0.5 にするとそうなります．しかし，これは非常に特殊な場合になります．つまり 0 〜 1 間の実数を適当に指定したとき， 0.5 になる確率は 0 です．従って，最終的に 0 に収束する確率も 0 になります．
- ロジスティック写像への変数変換は直感でやるしかないのかと疑問に感じました．
- 今回紹介した変換は， Rとbの比をとっているので，比較的思いつきやすいかも知れません．これはあまり本質ではないので，気にしなくても良いです．
- 授業には関係ないと思いますが，周期の境目には何がおこるのでしょうか？
- ごめんなさい．周期の境目ということばの意味が良くわからないです．次回，もう少し詳しく説明してもらえますか?
- 周期1が不安定になって，周期2．周期2が不安定になって周期4．だったらカオスというのは周期が一応存在するのでしょうか．あと，RN_{t}(1-N_{t})=N_{t}の時は固定で良いのかが気になりました．
- 講義のときには少し触れましたが，周期が無限大になると考えるのはどうですか．あと，後半の質問の意味が良く掴めないので，次回詳しく説明してください．
- 1年のときの授業で，カオスが出てくるのは0〜１の間の無限小数が必要，みたいな話を聞いたのですが (たしかそのときは1/パイを例で使っていました)，特にそういう制約はないのでしょうか？意味が分からない質問だったらごめんなさい．
- お，良く覚えていましたね．素晴らしい．あのときにお話ししたのは，カオスの有する複雑さが，初期値の有する実数の複雑さに対応するというお話でした．なので，初期値を1/πにしたのだろう，と解説しました．
- カオスでは同じ値は出ないということが，なぜわかるのですか？
- お，鋭いですね．これについては，次回以降で説明します．
- ロジスティック写像で， R=4に近い値では周期2^{20}とか周期2^{20}とかも出てくるのでしょうか？
- 少し勘違いしているかもしれないので確認をしますが， R=4 のときだけがカオス的応答になるというわけではありません． R=4 に近い値(これも正確にはどの程度なのかが問題ですが) でも，カオスとなり得るので，周期が無限に長くなり得ます．
- ロジスティック写像において， x_{t} ＜ 0, 1 ＜ x_{t} の時を考える必要はないのだろうかと思いました．
- パラメータを 0 ＜ R ＜ 4 にすると， 0＜ x_{t} ＜1 となることが分かります．逆に，4 ＜ R にすると， 0 ＜ x_{t} ＜1 とならずに，発散してしまうので，通常は 0＜ R＜4 の場合を考えます．このような差分方程式は，区間力学系といわれています．
- R＜4の場合はどうなるのでしょうか？？
- 上の質問に対する答えと同じですが， R＞4 になると，状態値が [0,1] を越えてしまい，発散してしまいます．
- なぜ，R の(値？)によって収束や，周期や，カオスにわかれるのかが，いまいちつかめなかったので，その判別方法を知りたいと思った．
- とても良い質問です．次回以降でお話しできると思います． R についての規則も存在ます．
- ハエの個体数が非線形であることはわかったんですが，本当にN_{t+1}=(R-bN_{t})N_{t}で表せるんですか？
- 仰有る通り，これでハエの個体数が表せるかどうか，分かりません．が，少なくとも，線形な差分方程式では表せないことは一番最初に見せたハエの個体数の変化が，線形な差分方程式の作り出し得るパターンとは異なることからも分かります．
- 非線形な方程式なら何でもカオスがでるのか疑問に思った．
- これも良い質問．何でもカオスがでるわけではありません．実際，ロジスティック写像のパラメータ R が 1.5，2.9，3.3，3.52 の場合はカオスではなく，それぞれ，固定点，固定点， 2周期，4周期となることを講義中には紹介しました．
- この授業ではフラクタルは扱わないのですか？
- 講義予定では扱わないことになると思います．時間がとれそうにありません．すみません． ==＞と思いましたが，現在考慮中です(5月26日)．
- 実際にある事象の予測が本当に可能ですか？できるとしたら，カオスのような安定でない動きからどうやって数値を予測するのかまだわからないです．
- これもとても良い質問ですね．もちろん，ある事象がどのようなものかによりますが，仮にその事象が複雑な動きを示していても，その背後に決定論的な非線形なダイナミカルシステムがあるとすれば，そして，その背後に潜む法則 (ダイナミクス) を抽出できれば，予測できます．そのための方法論は，残念ながら，この講義では触れることはできないと思いますが，カオス的な振る舞いを示す動きを予測する手法は最近とても注目されている大事な課題です． ==＞と思っていましたが，少し触れるかもしれません．現在考慮中 (5月26日．)
- カオス的な不規則なデータから式を導くのは不可能に思えるんですけど，可能なのですか？
- 対象がカオスだとすると，非線形なシステムから生み出されたことになります．非線形な関数は無限次元となるので，この意味において，式を明示的に導くことは困難です．しかし，式を導くのではなくとも，観測されたカオス的な不規則なデータから法則を抽出するための方法論は最近かなり整備されてきており，その結果，かなりの高い精度で予測することも可能となっています．
- 前回の宿題になっていた演習の答えも教えてほしい．
- 演習の答えなどは，講義中に説明しています．

5月10日
- R=1のときは安定でも不安定でもないんですか？固定点の判断もできないですよね？
- 講義中にも説明しましたが， R=1 のときは中立といいます．「固定点の判断」というのが不明ですが，「固定点の安定性の判断」と解釈すれば， (これも講義で説明しましたが) 安定に含めます．
- ロジスティック写像において，Rの範囲はなぜ0＜R＜4なのですか？
- すでに，このFAQでも説明しましたが， Rの範囲を0＜=R＜=4 にしないと，状態値 x_t が発散するからです． 0＜=R＜=4 であれば，0＜= x_t ＜= 1 となります．
- 少しプロジェクターが見づらかったので，教室の前の方はもう少し暗くしてもらえるとうれしいです．
- 了解しました．次回からは気をつけるようにします．
- 固定点が安定か不安定かがどういう意味を持つのかいまいちわからないので，来週からが楽しみです．
  安定だと何か良かったり，不安定だと何か悪かったりするものなのですか？
  固定点の安定性を知ることによって，何がわかるのかよく理解できなかった．
- 固定点が安定であれば，最終的には，その固定点に収束します．一方，固定点が不安定であれば，その固定点には収束しないので，おおざっぱにいえば， x_t がどのような振る舞いを示すのかを知るための指標になり得ます．
- ロジスティック写像の固定点の安定性を式で解いて表した結果が，ずいぶん前にやった図式解法の結果とぴったりで，なんだかつながって気持ちよかったです．
- それは良かった!
- 大域的と局所的安定性というのは，厳密に異なるときがあるのですか？
  分岐の境目はどうなるのか？
- 大域的安定性と局所的安定性は異なります．ただ，ロジスティック写像の場合は両者が同じになります．「分岐の境目」については，次回詳しく説明します．
- x^{*}=1-1/RでR=3.52のロジスティック写像を見てみると，局所的には不安定ですが，発散していないので，指数関数的に発散と言っていいのかわかりません．何を分岐というのかわかりませんでした．
  R=3で分岐するという使い方で良いのでしょうか？
- 確に固定点 1-1/R は不安定ですが，そのかわり，2周期解が安定になるので，状態値 x_t は指数関数的に発散しなくなります．分岐というのは，パラメータ(ロジスティック写像の場合R) を変えたことにより， x_t の振る舞いの質が変ることをいいます．「R=3で分岐するという使い方」でOK．
- ロジスティック写像に写像において， Rとdf/dx|_{x^*}の値には何か関係はないのですか？関係はなくとも，何かカオスの性質に関わる特殊な性質が，そのときのdf/dx|_ {x^*}の値にあると思われるのですが．
- 講義中に説明したように，もちろん関係があります．
- y_{t+1}=my_{t}のmの値による安定性の場合分けについてですが， m=1,-1,0の場合は議論しなくても良いのでしょうか？
  2つ以上の定数が含まれる場合の安定性がどうなるのか気になりました
- 講義でも説明しますが，このときは丁度中立になります．二つ以上の定数が含まれる場合も同様です．
- ロジスティック写像の例では，安定や不安定のとき，０でない方の固定点周りで収束したり，周期解を取ったりしていましたが，０の回りには行かないんでしょうか？初期値が０のときだけですか？
- 0＜=R＜=1 では，0という固定点は安定なので，0の回りにはいきますが， 1＜R では，0という固定点は不安定になります．
- 自然界の現象がカオスで表せるなら，そこで固定点はどういう意味を持つのかと思った．
- 実は，カオスには，無数の不安定な周期解(固定点を含めて)が埋め込まれています．
- 今回取り扱ったのは，すべて大域的安定性で良いのでしょうか？
  局所的に安定とは固定点に収束する初期値が一つでもあれば，局所的安定なのでしょうか？
- 講義でも説明しましたが，ロジスティック写像の場合，大域的安定性と局所的安定性は同じです．初期値が一つというイメージではないですね．
- Rが少しずれるだけで，固定点の安定，不安定がかわってしまうという微妙なラインがあまり納得いきませんでした．
- それでは，次回以降，再度詳しく説明することにします．
- *とtが混ざってよくわからない部分があったので，細かい部分はペンで書いてほしいです．
- 了解しました．
- 非線形の方が場合分けでいろいろな振る舞いをするので面白い．
- さすが，その通りです．

5月17日
- 0と1のあらゆる系列が(0,1)の間の初期値で表せるのは，実数の密度が非常に高いことを反映しているように思いました．
  決定論的でありながら，なぜ予測ができないのかについて，詳しく知りたいです．
  質問
  たとえば，2周期解が安定な場合， 4周期以上の解の安定性はどうなるのでしょうか？
- いずれも鋭いコメントですね．予測不能性については，次回説明しますが，初期値に鋭敏に依存する性質がその元になります． 4周期以上の解の安定性については，その次の回あたり説明しますが，2周期解が不安定化すると同時に， 4周期解が安定化します．
- 予測が「難しい」のではなく，予測が「できない」のでしょうか？
  ルールが決まっていて，且つ，決定論なら予測は（極限まで精度を高くすれば）可能に思えます．
- 鋭いコメントですね．答えは「困難」ですね．仮に，初期状態を無限の精度で観測し，モデルに対する完全な知識を持っていたら，予測できますので，仰有る通り可能です．
- 決定論的なものを確率で予測できるとなると，これからの世界がまるっきり変わってくる．ものすごいことだと思う．
- 決定論的なものを確率で予測できるということは言っていないですが．．．いずれにしても，ものすごいものではあります．
- 例えば，たまたまx_{100}とx_{300} が同じ値になってしまうことはないのでしょうか？
- この「たまたま」というのが起きたとすれば，それは周期が200であったということになりますね．
- カオスの持つ非周期性に関して，アナログ性が大事と言っていたのはどういうことでしょうか？
  計算機で表現できない連続的なレベルに置いて，常に唯一であると保証されているということですか？
- おー，これまた鋭い．その通りです．ディジタルでは結局有限周期なものしか表現できませんので．
- 因数分解ができませんでした．うまくやるこつはあるのでしょうか？
  また，一次元写像x_{t+1}=f(x_{t})に対して， n周期解を考えるならば，なぜ，x_{t}対x_{t+n}について考えれば良いのか，よくわかりませんでした．
- 因数分解ですか・・・今回の場合について言えば，図式解法でも照会したように，かならず 0 と 1-1/R を因数に持つので，それを頼りにするのが良いと思います． n周期解とは，x_t をfでn回写像した後を考えることになるので，それは x_{t+n} ということになります．
- 決定論的なのに確率的なものが作れるなら，未来におこることを予測する幅が出てくるかもしれないと思った．
  異なる初期値を与えて，同じ挙動を示すことは全くないのだろうか？
- 鋭い！確に予測にたいするオプションが増えると言えます．もしカオスでなければ，異なる初期値を与えても同じになりますが．
- 初期値鋭敏依存性が「ある」と「ない」の境界はどこですか？
- 安定性の定義で照会した関数形の傾きの絶対値が1よりも大きい，というのが元になります．全ての点に対してこの傾きを求め，その積が1よりも大きければ，初期値鋭敏依存性があるということになります．これを表す尺度はリアプノフ指数と呼ばれています．
- ほかの3つの定義は満たしているのに，カオスでないものはあるのですか？
- 例えば，乱数がそうですね
- コイントスはカオスによって再現できるということですか？
- その通りです．
- R≠4のときの8周期解とかの図も見てみたいです．
- これは，分岐のときに照会する予定です．
- R=4がカオスになるということは極限R＝＝＞4のとき， n＝＝＞無限大が成り立つという発想で正しいですか？
- 「n＝＝＞無限大」というのが，周期が無限になるということでしたら，正しいと思います．
- コイントスで無限回，表を出し続けるときもあると思いますけど，そこいらへんも再現できるってことですよね？
- できます．
- 量子力学が絡んでくるような場合でも，決定論的な理論は成り立つのですか？
- おおー，すばらしい意見ですね．不確定性原理が発現すると思うので，今，紹介している話がストレートに使えるということにはならないと思います．量子カオスという研究分野もありますが，重原先生がご専門です．
- なぜ確率的なものを再現できるのか，いまいちわかりませんでした．
- 了解，次回に再度!
- 「ルールが定まっているのに（そのルールがわからないから）予測できない」ということですか？
  それとも「ルールがわかっていても」予測できないという意味ですか？
- 仮にルールを完全に知っていても予測できないですね．初期状態の観測精度の有限性に由来しているので．
- カオスの「定義」を４つみたすものなら，どんなものでもカオスと言い切れるのですか？
- 今日紹介したのはあくまで「"定義"」です．カオスであれば， 4つの性質を満たすぐらいに思っていてください．
- R x{x-(1-1/R)}{R^{2}x^{2}-(R^{2}+R)x+(1+R)}=0の最初の Rはなくて良いのですか?
  あと，x=1-1/Rをどうやって導出するのかわかりませんでした．
- Rはあってもなくてもよいですよね．因数分解により求めたいのはxの値ですから．また，x=1-1/R の求め方については，講義で説明しています．これまでに配布した資料なども参考にしてください．
- 任意のFR系列に対応する初期値が存在するとのことでしたが，ならば，すべての事象を適切な値域における状態の当てはめができれば， x_{t+1}=4x_{t}(1-x_{t})で表すことが可能になるのでしょうか？
- ごめんなさい．ちょっと意味がわからないので，直接議論しましょう．
- やっぱりカオスが一番面白いと思った．
- その通り!良く理解してくれました．

5月24日
- ロジスティック写像の分岐図がわからなかった．途中からの動きがわからない．
- 来週もう一度説明します．
- ロジスティック写像R=3.8のあたりで，点の数がかなり少なくなっているが，これは何を意味しているのか疑問に思った．ロジスティック写像の分岐図で空白になっている部分は何を表しているのですか？
- 鋭いですね．これは周期の窓と呼ばれています．この窓の出現についても，規則があるのですが，これも次回以降に照会します．
- ひも理論は三大発見に入らないのか気になった．
- 講義中に紹介した20世紀の3大発見というのは，ジェームス・グリックという人が書いたカオスという本に紹介されているのです．
- 三体問題はカオスを用いて解く事はできないのか？
- 「カオスを用いて解く」というのがイメージが湧かないのですが，三体問題にはカオスが存在するという方が正しいイメージですね．
- 今日の講義は楽しかった．
- どうもありがとうございます．今日の講義以外はどうでしょう?
- 今日は，カオスについて言葉や式だけでなく，実際に自分の目で見たりする事ができて，「おもしろさ」を体験でき，よかったです．
- それは，良かったです．これからも楽しんでください．
- カオスは予測不能とありますが，長期予測でない予測もできないという事ですか？
- もちろん決定論敵なので，短期的には予測可能になります．
- ロジスティック写像を0＜x_t ＜0.5 ＝＝＞表と二値化したときに，表表表…が表現（確率的な事と対応）できないように思います．
- 0＜＝x_t＜0.5でしたね．こうすればできますね．
- 例えば，機械的にコイントスを繰り返す装置があるとして，１００回試行結果を得たとして，決定論的に１０１回目のコイントスの結果を予測しようとしても，カオス理論だと，１００回までの試行をそのまま再現した上で，１０１回目がおもてになる初期値，裏になる初期値がそれぞれ存在するはずだから，結局未来の予測は確率論にしかない得ないのではないでしょうか？
- うまく質問の意図を理解できているか不安ですが，長期的な予測は確率的にしかできないことになります．
- コイントスもさいころもよく考えてみると，それは投げた瞬間に定まるという決定論的な発想は，なんとなく理解できた．
- 今日話したのは，こういうことではありませんでしたが．
- 表と裏の二文字は似ているので，「米」と「＿」といった，視覚的に違いが見やすい記号を使うべきだと思います．
- 了解です．次回からは変更します．
- 振り子を三重，四重，…にするとどのように振る舞うのですか？カオス解になるのですか？
- カオスになりますね．2重でもなりますので，
- それぞれの単振り子について運動方程式を組み立て合わせれば，うまくすれば物理的には二重振り子の振る舞いを表す事ができるような気がするが，そんな事ができないのだろうか？そうすればカオスを方程式で表す事ができるような気がした．
- 出来ます．
- 証明についてもちょっと聞いてみたかったです．まあ，ちょっと…．
- それじゃ，特別に宿題にしましょうかね．
- 観測精度の限界は，不確定性原理によるものでしょうか？
- 一般的にはそうなるかもしれませんが，今日の話では，不確定性原理に直接起因するということではないです．通常，我々が行う計測・観測という行為においては，ある状態値そのもののの精度は有限となります．
- コメントを書く時間が少し短い気がします．
- ごめんなさい．次回からはもう少し早くから配る事にします (TA保坂)．
- 絶対にあり得ない事ですが，初期値が完全にわかっていれば，カオスでも長期予測ができるという事でしょうか？
- はい，出来ます．その通りです．良く理解できていると思います．
- カオスマン面白いです．ぜひ下さい．
  カオスマンが欲しい．
- 確にカオスマンはおもしろいのですが，差し上げるのはちょっと・・・二重振り子自体は簡単に作ることができるので，挑戦してみたらどうでしょうか．
- カオスが嫌いな先生がどうしても気になるので， HPでこっそり教えてください．
- さぁ，僕は知らないですね・・・カオスや非線形が大好きという(心が真っ直ぐ)な先生たちなら，沢山知っていますが．(^^)

5月31日
- ロジスティック写像の x_{t+1}=Rx_{t}(1-x_{t}) という式はどこから出てきたのでしょうか？
- これはこの講義の最初に既に説明しました．
- 今日のレジュメのp.25の一文に字が抜けている箇所を発見しました．
  「今日も講義開始時に，A4用紙一枚(表裏使用可)で提出してもらいました．」
- どうもありがとうございます．今後もこのような指摘も含めて，問題があれば言ってください．対応できるところは対応します．
- R→4の時，周期→∞となって，これがカオス，という理解で良いのでしょうか？
- R=4 じゃなくてもカオスになるので，ちょっと違います．次回，再度説明します．
- グラフとの交点など，「ぱっと」イメージがわかない事が多い感じです．
- イメージが湧かないということであれば，質問是非してください．もし質問があれば，あるいは，分からなければ，すぐに手をあげてもらえればよいと思います．あるいは，不安そうな顔をするとか，ちょっとヤバイという視線を送ってもらえれば，その都度説明を繰り返すようにします．
- 最近演習の時間がどんどん減ってきている気がします．
- 了解です．確に仰有る通りなので，次回はたっぷり演習をやってもらいます．
- カオス解で二度と同じ値が出ないというのは，実際にはn周期解で， nがものすごく大きな値であるという事なのですか？
- ものすごく大きいのではなくて，無限大ということです．
- 周期倍分岐の他にもカオスになるルートというのが存在するのですか？
- おおー，とても良い質問ですねー．あります．ただ，この講義では分岐の話を詳しくすると，みんなにとって少し大変だと思うので，詳しくは触れないです．大学院の講義 ( 非線形システム特論 ) で詳しいことを解説する予定です．
- ○どこを境にカオスになるのですか？
  ○ロジスティック写像において， Rの値がいくつになったときにカオスになるのか疑問に思った．
  分岐の実験例として，R=3.9でカオス解とありましたが， ○R＜4でもカオスになるのですか？
  ○厳密にはRの値がどれのとき初めてカオスになるのですか？
  ○カオス解は R=4 より小さいうちから出るという事ですか？
  はい，ここからカオス！って言うにはどうやって出てきたんだろう？と思いました．
- これらの質問については，次回詳しく説明しますが，周期倍分岐の起きるRの点は次々と早くなり，ある値に収束します．その値以降ではカオスとなり得ます．
- 昨日の夜の時点では今日の最高気温は28度と言っていたのに，今日の朝は24度になっていました．例えば天気予報では，どのくらい近い未来ならカオスで100％予測できるのですか？
- 何事もそうですが，100パーセントというのは難しいですね．でも，カオスというか，非線形性ですね，それを考慮することにより，単なる線形な予測方法よりは，予測精度は向上します．
- 帯状に空白になっている部分には特に意味はあるのでしょうか？
  R=3.85あたりが特に，出てくる周期が急に減っているようですが，どういう事なんでしょうか？
  分岐図をみると，R=3.62, 3.75, 3.82付近に周囲とは雰囲気の異なった周期解のような分岐があるのですが，これは特別なものなのでしょうか？
- はい，あります．窓と呼ばれているのですが，これについては，次回コメントします．
- f^{2}のグラフの交点で2周期解 (4周期解) が現れているのかがわかるなんて，よくできているなぁと感心してしまいました．
- そうですね．良くできていると思います．
- 2^{n}周期と2^{n+1}周期のグラフに， 2^{n-1}周期と2^{n}周期のグラフが同じ形が出てくる事がピタッとはまった気がしました．分岐図の解の間の幅の差のなぞも，f^{2},...,f^{n}の関数系を見てなるほどと思いました．
- ピタッとはまってもらって良かった! ちゃんと理解してもらえたようでよかったです．
- 先週休んでしまいデモが見れなかったので，またやってほしいです．
  3重振り子のデモも見てみたいです．
- 了解です．次回は，電気回路のデモをやります．３重振り子は手元に無いので，デモはちょっと難しいですね．自分で作ってみてください．
- コメント用紙の配布が早くてよかった．
- 保坂君，今後もよろしくお願いします．
- カオスは本当に混沌としたものでない事がわかりました．
- GJ!
- ロジスティッック写像の8周期以降の絵がわからない．点がバラバラにあるのでしょうか？
  グラフの塗りつぶしたような部分がよくわからない．
- バラバラということではないです．拡大すると8の次は16， 16の次は32というようになります．「グラフを塗り潰したような部分」は，その間の色々な値を取り得るということで，カオス的ということになります．
- 「R=3で不安定になり始める」という表現は， R=3では安定でも不安定でもないという事でしょうか？
- 丁度，境目ですね． f'を計算すると丁度-1 になりますので．
- 固定点の不安定化→新たな安定点の出現の流れに”軽く”感動しました．
- 「軽く」ですか．もっと感動してほしいですね．
- 分岐図を見ても， 2周期が消えて4周期が現れるタイミング， 4周期が消えて8周期が現れるタイミングはすべて同時に起こるようですが，偶然には思えません．何か理由があるんですか？
- 講義で説明したように，理由があります．
- 周期解がいくつか混在する時があったり，周期解がない時もあるのですか？
- 混在ということですが，安定でないものと不安定なものは，同時に存在し得ます．「周期解がない時」というのが分かりにくいですが，周期が無限であるときということであるとすれば，もちろんあります．
- 分岐図は固定点の集合と考えれば良いのでしょうか？
- 固定点のところもあれば，2以上の周期解もあれば，カオス解もあります．
- Rの前後での安定・不安定の移り変わり，もとあった安定解の周囲2点への倍分岐が図を変化させながら見られたので，良いもの見たなぁと思いました．
- そうですか．そう思ってもらったのであれば，良いもの見せたなぁという感じです．
- 2周期解から4周期解に移る時の図が，固定点から2周期解に移る時の図の自己相似形になっているのはフラクタルと関係があるのでしょうか？
- はい，関係があります．さすが，良く気づきましたね．次回紹介します．
- 前回の講義の事なんですけど，例の「確率論＝＝＞決定論」の話があれから妙に気になって，いろいろ考えてました．
- 考えることは良いことだと思います．一度じっくりと議論しましょう．
- コンピュータでカオスをシミュレートする際，扱えるデータが有限桁である事は障害にならないのでしょうか？
- なりますね．講義でも説明したように，カオスはアナログの世界の複雑さを表わすと考えることもできるのに対し，我々の現在使っているディジタルな世界のみを対象としています．で，障害になるとして，どうするの?という質問がでると思いますが，これに関する研究もあって，確かにディジタルでは本当のカオスをみることは，出来ないのですが，真のカオス軌道の存在に保証がなされています．

6月7日
- １，3周期が現れる前後の関係はどうなるのかわかりません．
  ２，分岐窓の部分はどうなっているのか疑問に思いました．
- を，いいですね．実はここにもカラクリがあることが分かっています．講義では触れませんが，例えば3周期の窓であれば， fの3回写像が鍵になるのは，もう分かりますよね．
- ロジスティック写像の分岐図がフラクタルである事と，奇数周期が出る事は矛盾しているような気がするのですが？
- どのあたりが矛盾するのか分からないので，今度直接話をしてください．
- フラクタルの要素に還元できないと言うのはどういう事ですか？
- 講義中に説明しましたが，線分などの(単純な) 要素に分解できないということです．
- フラクタルは内部相似を持つと言いますが，全体と限りなく小さいものでも相似になるのですか？
- そうです．ところで，内部相似という用語もあるのかもしれませんが，自己相似という用語をつかいました．
- いずれカオスになるような現象には必ずフラクタル性がカオスに至るまでの過程に出てくるという事で良いのでしょうか．
- カオスに至るルートには様々なものがあるので，必ずしもそうではないです．
- 分岐図において，フラクタル性が出てきて面白いと思ったが，フラクタル性になっている事でどのような事がわかるのだろうか？
  また，分岐窓が存在するが，これもフラクタル性に影響しないのだろうか？
- この場合，同じカラクリで分岐が起きていることの表れと捉えるのが一つだと思います．また，同じカラクリと分かれば，次にどこでその現象が起きるかという予測も可能になります．窓も多重に存在します．
- 分岐図におけるフラクタル性は本当に無限に続くのですか？
- はい，続きます．
- 今日のデモで身近にカオスが偏在しているという事がわかりました．
- それは良かった．
- コメントの時間も欲しいです．
- 次回からは保坂君に早めにコメント用紙を配ってもらいます．
- 久しぶりにこんなに頭を使いました．
- 来年になれば，もっと頭を使うこと必至なので，今から使うようにしておきましょう．でも，今までの講義ではそんなに使わなかったのでしょうか．
- f^{2}(x)=0の解を見つけいる事すらできませんでした．
- これはかなり前にやりましたね．前のプリントを復習してください．
- 演習がよくわかりませんでした． 4周期解を求めるってことは，固定点が４つ出てくるってことですか？
- 多分，教室の後の方に座っているからだと思います．また，宿題を写しているからだと思います．次回からは前に来てください．
- あまり計算をさせないで欲しいです．苦手なので．
- それほど計算させていないと思いますが・・・でも，計算が苦手ということはないと思いますよ．みんなの場合．仮に計算が苦手だとして，その場合は，自分で苦手と思わない方が良いです．ますます苦手になるから．
- 問題を一度全部解いて，まだ理解できてないところがあったら改めて質問します．
- 是非そうしてください．分からなければ，講義以外の時間でもどうぞ．
- ファイゲンバウム定数の凄さがいまいちわからなかった．
- うーん，そうですか．それでは次回再度説明します．
- 2次関数の代わりにsin関数などもファイゲンバウム（普遍）定数が有効なのですか？
- 多分大丈夫だと思います． 2次できんじできるだろうし… 今から確認の計算してみますが．
- いったい何が，ファイゲンバウム定数のような多分野に共通する「値」を決定しているのかとても興味深い．.
  この宇宙を定めるものとは何なんであろう
- 次回の講義で説明しますが，写像関数がある条件を満たすと(条件といってもそんなに特殊ではない)，ファイゲンバウムの普遍定数が観測されます．
- 前回の演習の解説を一人一人やってくれたのには驚いた．
- それでは，最終課題の提出時も，一人一人の提出にして，口頭試問をおまけにつけることにしましょう．
- 前回のレポートで，Rがちょうど1,3になる場合，どのように説明するのが良いのでしょうか？
- 安定でよいと思います．
- ある現象が「カオス」であるという事と，「カオス的な応答を示す」という事は同じ事なのでしょうか？
  そもそもある現象が「カオスである」とは正しい日本語でしょうか？
- 定性的には同じこととして使いました．後者については間違っていないと思います．
- 下図の○で示したところはどんな事になっているのですか？ぱっと考えるとこの辺の方が奇数周期解になるのかなと思っていたのですが．
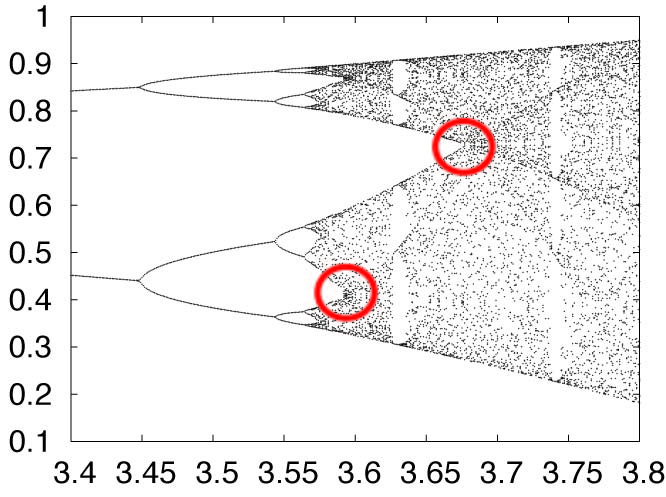
- 奇数周期解は，例えば，その右側にある5周期の窓などの場所ですね．この場所は，幅が広がっていって，それまで島に分かれていたところがぶつかる箇所に相当します．

6月14日
- 「張り付ける」という表現は「貼り付ける」の方が正しいのではないでしょうか．
- を，鋭い指摘と思い，北原保雄先生(因に，池口の高校の大先輩) の明鏡を調べましたが，間違ってはいないようです．ただし，「貼る」の方が好まれるとありました．
- フラクタルがカオスとどのへんが関係があるのかよくわかりません．
- 前回までに，カオスの分岐図を紹介しましたが，ここで全体と同じ構造がでてくることを紹介しましたし，今回の講義でもその説明から入りました．
- 長さ0（無限小）を持つ線分を点と認識すれば，今回の事もあまりおかしいと感じないかもしれません．それは認識としておかしいのでしょうか？長さ0を持つ線分（点）の集まりがカントール集合と考えれば矛盾しない気もします．
- それでは，普通の線分はどう考えますか?
- 点は長さが0なので矛盾はしてないんじゃないですか？
  もっといろいろなフラクタル図形が見てみたいです．
- でも，個数を数えると無限個あるんですよ．フラクタルの参考書は次回紹介予定です．
- 平面幾何では，点は長さや面積や体積を，線は面積や体積を，面は体積をそれぞれ持たないので，（点，線，面）がたくさんあったとしても，（線，面，体）が存在していなくても矛盾していない気がします．
- 後半の「矛盾」というのが，前半から導けないと思うのですが，いずれにしても，僕が講義中に使った「矛盾」という言葉が悪かったかもしれません．次回再度説明します．
- 池口先生は画像圧縮技術も研究しているんですか？
- 僕自身は画像圧縮についての研究はやっていませんが，次回の講義では紹介する予定です．
- 無限を扱う事の難しさが身にしみてわかりました．カオスも同様な難しさがあると思うとぞっとします．
- いいところに気づいていると思います．確かに無限は難しい．そして，カオスは難しいかもしれませんが，理解していけばとても面白いことに気づいてもらえると思います．
- なんでこのような矛盾を起こすのかとても不思議です．集合の長さを求める計算も，理論的に間違っていないのに…．次回の講義が楽しみです．
- 是非，楽しみにしていてください．
- 点とか長さという概念だけでははかれないものがあるということが興味深かった．
- そうですね．非常に大事なことを理解してもらったと思います．
- 「カントール集合上の点の数はI=[0,1]上の点の数と同じ」という意味がまだちょっと分かりません．
- 3進法を使ったところですが，次回再度説明します．
- 極限的に考えれば，０×∞＝０になる事もあるので， L_n→０と無限個の点があるという事は，特に矛盾していないと思います．
- 「極限的に考えれば，０×無限大＝０になる事もある」ということと，「L_n＝＞０と無限個の点があるという事」はこの場合，関係ないと思いますが，いずれにしても，次回再度説明します．
- 途中から講義のスピードが速くなってわかり辛かった．
  後半速くて辛かったです．
- すみません．今日は，そのような認識は僕自身はありませんでした．次回からは気をつけます．
- フラクタルであれば，カントール集合上の点の数と長さのような矛盾が必ず出てくるのでしょうか．
- そうですね．でてくるといって良いでしょう．
- よく極限まで持っていくと0になるみたいな事を習ったりしたが，自分は絶対に0になり得ないと思っている．
- うーん，それは困りましたね．でも，確かに「極限までもっていく」とか，「十分に近づける」っていうのは，非常に曖昧なんですよね．なので，イプシロンーデルタ論法などを再確認するのはどうでしょうか．
- 長さが0なのに，点の個数は無限というところがイメージが持てず，難しかった．
- 了解，次回もう一度説明します．
- 実験はフラクタルをやらないんですか？
  本当に？
  残念です．
- まだ分かりません．でも，なぜ残念？もう単位はとったでしょ．
- A君は39度を超える高熱で早退しました．それでもがんばってきたので，許してあげてください．
- 許すも許さないも，次回からちゃんと出席してくれたら良いです．
- 同じ事を繰り返しているだけなのに，とても複雑なものへとなっていく感じが不思議な感覚で面白いと思いました．それとは逆に，とても複雑に見えているものも，単純なものからなっているという事は，いろいろな事（形だけではなく，生活の中などでのいろいろな事）に通じているかもしれないなぁ…と考えてしまいました．
- そうですね，このように「単純」なものに分解できるというのは，とても大事な考え方の一つだと思います．しかし，カオスやフラクタルの重要性は，このような「単純」さに分解できないというところにあります．
- なんで[0,1]の区間の実数を３進数で表すんですか？
- 講義中に説明したように，カントール集合の作り方が，3進法と関係するからです．
- 正しいことを言っているのに，矛盾した結果になってしまうのは面白い結果だと思った．
  どういう仕組みでそうなるかが気になる．
- 気になるのは，とても良いことだと思います．このまま，色々なことを気にするようにしてください．

6月21日
- 例に出てた4つ (カントール集合など) 以外にもフラクタルなものには各々次元が存在するという事ですよね？
- はい，その通りです．
- 3次元と4次元の間にも次元は存在するのですか？
- もちろんあるでしょう．ただ，我々に想像できるかどうか．なにしろ3次元を越えていますので．
- 複雑ネットワークの回で，フラクタル再来はありますか？
- スケーリングという意味では関係あります．
- ○CGのところで，どこにフラクタルを用いているのかわからなかったのですが…．
  ○CGの応用において，どのようにフラクタルを実現したのか気になります．
  ○CGへの応用などの具体例をもう少し話してほしかった．
- この講義はCGの講義ではないので，詳しく触れるつもりはありません．興味がある場合は，自分で調べてください．
- 線分や正方形は，ぴったりとすべてが覆われているからわかるのですが，フラクタル図形のところがいまいちわかりませんでした．
- そうですか．それでは次回再度説明してみますが，自分でもよく考えてみてください．
- コッホだけ1次元の線から，次元が増えて， 1.21(?6の間違いか?) 次元を作り出す事ができるようですが，立体を上手に使えば，3次元以上のものを作り出せるのでしょうか? 4次元，5次元以上のものを…．
- 非常によい質問ですね．仰有る通り，できます．今回紹介したフラクタル図形のうち，コッホ曲線だけが作り方が別です．良いところに気づいたわりには，次元の計算間違ってますね．
- そもそもある処理を無限回繰り返して作る図形というのは，実際には存在し得ない図形なのだから，そのような図形について，次元が整数値でないなどといった考察をしても，こじつけのように聞こえてしまいます．具体的にどのような利点があるのでしょうか？
- 講義でも説明したように，こじつけではないですね．実際に存在する図形ですので．
- 自然な尺度でカントール集合等を測ったときに収束する値というものがいったい何を表す値なのか気になりました．
- この場合は，どの尺度が良いかということを考えていることになります．
- ハウスドルフ測度というのは，カントール集合のみにいえる自然な尺度ですか？
- いえ，そうではなく，フラクタルな図形を含めて，点，線分，正方形，立方体なども含めた場合にうまく測ることができる尺度になっています．
- カントール集合が自然な尺度で収束するが， 1とか2とかきちんとした数字で表す事は可能なのか？
- 「1とか2とかきちんとした数字」というのが何を表わすのか不明ですが，カントール集合にとって収束する場合の尺度の次元が0.63... ということです．
- 次元が非整数のものがあるという事が普通に考えれば考えられる事だけれど，実際に目の当たりにして不思議な気分でした．
  図に表すとどうなるのでしょうか？
- 図に表わすと，今日紹介したフラクタル図形がその一例ということになりますね．
- 一般的な整数次元とフラクタル次元の違いがわかりません．
- 講義では，非整数値を取りえる次元のことを，フラクタル次元と呼ぶことにしておけば良いことにしました．
- 点，線分，面積，体積などは整数次元はx軸， y軸，z軸などを使った表現する事ができますが，非整数次元もこのような表現方法はあるのでしょうか？
- 軸を使うということはちょっと難しいかな．
- 次元が非整数とはどういう事なのかよくわからなかった．日常で非整数次元というものは存在するのですか？カントール集合などの次元を求めて何か良い事があるのですか？
- 講義でも説明したように，例えば，　0.63次元というのは，複雑さの度合いが丁度0次元と1次元の中間，というように考えてみるのはどうでしょうか．今日紹介したフラクタルは，幾何学的に厳密な意味で自己相似構造を持っています．一方，我々の身の回りにある複雑な形状 (例は前回の講義で紹介しました)も，自己相似的な構造を持っていますが，これは，統計的な観点からの自己相似性です．そこまで自己相似を拡張すれば，確かに存在しますね．そして，このようなフラクタルなものが実在するのであれば，その複雑さを定量的に表現しようとする次元は十分に意味があることになります．
- 4次元なものを測る為の尺度って何ですか？
- 4次元体積かな．
- 3次元までの測度はすんなり実感できるけど，それよりも大きい次元になるとどうなるんですか？
  関係ないけど，宇宙は10次元？11次元？
- どうなるんでしょう．僕にも実感できません．普通の人はそうだとおもいます．
  宇宙のことは知らないです．
- 0.6309…次元とかいわれてもいまいちピンと来ません．フラクタル次元にもm^{1}やm^{2}見たいにm^{0.6309…} のような単位とかはあるんですか？
- 確かにピンとは来にくいですね．単位ですか．今回は元々無次元量を扱っているので，無いですね．
- 次元がマイナスの値になることはあるんですか？
- をっと，面白い質問ですが．僕は聞いたことが無いです．
- フラクタル次元が0.99999999999999…というように限りなく1に近いとき，長さはどうなるのでしょうか？
  1になった瞬間に線分の長さLになり，そうでなければ0なのでしょうか？
- うーん，難しい質問ですね．ちょっと考えます．
- ○ベクトル量子化や離散コサイン変換のイメージがわきませんでした．
  ○フォトニックフラクタルはエネルギーが蓄積されるという事なのでしょうか？
- この講義は画像の講義でないので，詳しくは説明しません．興味があれば自分で調べてみましょう．
  フォトニックフラクタルについて，詳しくは知らないのですが，そういう感覚でも良いのかもしれません．
- 長さや面積は同一次元の他のものとの比較に使う尺度だと思うのですが，ハウスドルフ測度も同様の使い方をするのですか？
- これそのものが測度になるので，そういう使い方はしないと思います．
- フラクタル次元は整数値でないというメージが難しいです．
- 確かに難しいですね．イメージするのは．
- ○有理数もまた必ず離散的に配置される無限の点だと思いましたが，自分の認識が間違っているのでしょうか？
  ○完全にフラクタルである構造（無限に繰り返し）は理論上にしか存在しないものでしょうか？
- ○有理数に対する考え方はあっていると思います．
  ○今回紹介した図形は，幾何学的に完全に自己相似な図形ですが，「完全にフラクタルである構造」ということをそれだと解釈すると，我々は無限小まで観測することはできないので，その意味においては，理論的な存在といってよいかもしれません．が，これは必ずしも存在しないのだということを示すことにはなりません．
- コッホ曲線の面積の定義がよくわかりません．下の黒く塗った部分で良いのでしょうか？
- いえ違います．コッホ曲線で面積と呼んだのは，コッホ曲線の場合，線分が次々と織り込まれていくのですが，その線分の面積のことになります．
- 来週までにlog5について調べてきます．
- 講義が始まる前までに，ホワイトボードに書いておいてください．
- 「正方形の長さは無限大」，「立方体の面積は無限大」っていうのがどういう事なのかよくわかりませんでした．
- 正方形の中には，線分が無限個ありますよね．同様に立法体には，正方形が無原稿重ねられていると考えることができます．そのことを表現しました．
- スタートレックとかGIRL LENNAはどのへんがフラクタルなのでしょうか？
- 講義でも述べたように，スタートレックのなかで用いられたCGがフラクタルを用いています．また，これも講義で説明しましたが， GIRL，lenna は単なる標準画像です．これらがフラクタルということではありません．
- 基礎を学ぶ事の大事さはわかったような気がします．
- それは良いことです．応用，応用と叫んでも，基礎ができていなければ，砂上の楼閣．簡単に崩れ落ちますので，ご用心．それに，今，使われている技術をやっても，ダメでしょう．分かりますよね．
- フラクタルあたりは個人的にはカオスよりも面白く感じた．
- そうですか．個人的にはフラクタルよりもカオスの方が面白く感じます．実際は，カオス現象にはフラクタルが出現するので，これも個人的意見ですが，サブセットと思ってます．
- Physical Review Letters に掲載された論文の名前を教えてください．
- グーグルなどでPRLのサイトを訪れてください．埼大内であれば，サイトライセンスで，論文を自由に閲覧することができます．その際，著者名，ボリューム，ナンバーをいれるとすぐに検索してくれます．
- 先生は実は凄い人だと初めて知って驚いた．
- 僕は別に凄くありませんが・・・今までは，へんなおぢさん，って感じでしたかね．コメント用紙を読んでいると，皆んなの方が，とてもすごいと感じます．是非，大学院に進学して，もっと力を伸ばしてください．

6月28日
- 1次元では，Epsilon'/Epsilonを計算すれば良かったですが， 2次元では何を求めれば良いかわかりませんでした．答えは来週の授業でということでしょうか？
- そうですね．来週は線形写像の応答を考えます．
- エノン写像や池田写像にカントールやコッホみたいに，基本図形を1/mにしてn個くっつけるのような規則性を見つけられないのですが，「フラクタル＜＝＞基本を縮小して複数個配置」といった捉え方が，良くないのでしょうか？
- エノン写像の(アトラクタの)場合，カントール集合やコッホ曲線のように厳密な意味でのフラクタルではないのです．
- エノン写像の固定点が， (1-b)^2+4a＜0になるa,bの値のときは固定点は複素数になるのですか？その時は不安定化するのでしょうか？
- 普通は実数の範囲で考えるので，その場合は固定点は存在しないということになります．
- 安定条件を得る為に1000回もの写像が必要なのでしょうか？
- 質問の意味が良く分からないです．写像というのは，写像の繰り返し回数ということですか?
- エノン写像でx(t)^2と書いてありますが，池田写像で書いてあるようにx^2(t)という表記で統一した方が見やすいと思います．
- そうですね．そのようにしておきます．
- 授業中に示された2つの2次元の非線形写像は，とても興味深い模様を描いていたのですが，模様を描くという事は，それほど多くの点を取り得ないという事がではないでしょうか？
- いえ，二つ共カオスなので，点の数は無限ということになります．
- 池田写像は，砂糖を混ぜた後のコーヒーにポーションを落とした状態 (この状態にも非線形性があるんでしょうか）によく似ていると思いました．自分的には真円じゃ無い回転運動だし，パラメータ多そうだし，ありかなと．
- をぉー，なかなか鋭いですね．仰有る通り非線形ですね．ラグランジュカオスと呼ばれています．
- エノン写像や池田写像のデモンストレーションで使っていたのはmatlabでしょうか？拡大も早くていい感じでした．
  Matlabの亜種ですか？
- Matlab です．
- 池田写像は卒業研究でも使われているようですが，どのような特徴がありますか？
- 非線形性が高次であるというのが一つの特徴だと思います．
- 池田写像はカオスだという事なのですが，　　点分布の間にある隙間は，　　カオスの窓と同じようなものなのでしょうか．
- カオスの窓というのは分岐図での話なので違います．
- ○池田写像もエノン写像もプリントのような値の取り方でないと　　カオスにはならないのですか？
  ○サドル点での挙動は一般にどのようになるのですか？
- ○はい，そのとおりです．
  ○これについては来週説明します．
- エノン写像や池田写像について何もわからない．何の為にその二つがあるのか全然わからない．
- うーん，困りましたね．説明をちゃんと聞いていますか？講義中に寝ていると理解は出来ないと思います．
- テーラ展開をするうれしさが何度効いてもイマイチ良くわかりませんでした．
- 難しい非線形な関数をそのまま扱うよりも， 1次式(直線) として扱うことが出来たら楽ですよね．いずれにしても，来週再度説明します．
- テーラ展開すると何が良いのかが，いまいちピンとこなかったのですが，安定性を見る為にEpsilonの多項式として表現したいから，という事ですか？
- そうです．
- テーラ展開において，Epsilon=x-aというところの説明を聞き逃してしまいました．なぜEpsilon=x-aになるのですか？
  過渡状態を無視しない時の議論が気になりました．
- この場合，点aからの動いてxになったと考えるので，　　x-a が変位，つまり，epsilon ということになります．
- ３次元，３変数以降の非線形な差分方程式でも周期解の安定性などは同様な考えで良いのですか？
- 基本的に同様です．
- 今回の安定・不安定は図では見れないものなのですか？
- 　　図で見るというのが，どのような図をイメージされているのか　　わからないですが，書くことは出来ます．　　来週紹介します．
- ノイマルク・サッカー分岐とはどういう挙動の分岐なんですか？
- 写像のホップ分岐です．といっても分かりにくいですね．詳しくは，大学院での特論で紹介します (多分)．
- 池口先生の研究しているカオスもグラフで見てみたいです．
- 僕が主にやっているのは，実際のデータの解析なのですが，そういうことについては，最終回に紹介します．
- あの大きな教科書は後輩に欲しいと言われましたが，あげなくて正解でした．
- そうですね．本というのはとても大事なので．
- 応用解析学や線形代数の知識を全くといっていいほど覚えていないので，　　これからの講義は不安になった．
- 覚えている必要はありませんが，導きだせるようにしておいてください．
- 非線形の分野でも線形に帰着して解けるというのが，ピンとこないです．
- 局所的に考えれば，曲がったものも直線近似できますよね．
- 僕はなんとまだ応用解析学をとれていないので，今まで以上に死ぬ気で取りたいです．
- なぜ前期開講の講義を取らないのですか？

7月5日
- 式の計算ばっかりで今回の授業はちょっと頭が混乱しました．
- 寝ないようにしましょう．
- 一応は理解はできているが，何を教わっているのかわからなくなりそうだ．
- 教わっているのは，非線形ダイナミカルシステムについてです．
- 名前を覚えているだけで大丈夫なのでしょうか？ジョルダンとか．
- 知らないよりはましですからね．だって，一度習っていたら，思い出すことは可能ですし，どういう本を見直せばよいのかということもわかります．いずれにしても，，，遅刻しないようにしましょう．
- AP=λPというときに
  A=λとしてはいけないのですか？
  行列と定数というように形が違うものだからですか？
- 駄目です．
- AP=λPとなるPは無いが， A^2P=λPとなるような固有ベクトルは存在するとき，その固有ベクトルは何を意味するのでしょうか？
- ちょっとわからないですね．
- 逆行列をしっかり復習したいと思いました．がんばってついていきたい．
- 頑張ってください．
- あらためて，行列の対角化を順を追って学習できたので，自分の中でうまく筋が通りました．とてもわかりやすかったです�
- それはよかったです．
- 同じ内容を複数の先生から説明されるのはいろんな解釈が聞けて良い．
- そうですね．それが大事なことだと思います．
- 最近穴埋めの部分が多くて，板書にかかりきりになり，説明を聞くのが大変です．
- がんばりましょう．世の中，僕の講義のように甘いものばかりじゃ有りません．
- 今回くらい速いと板書が追いつかなくなって話が半分流れてしまうので，速い時は書く量を減らしてほしいです．
- 最初から寝ているからです．気合いを入れましょう．
- スライドをめくるペースが早かったので，もっと遅くするか，書く量を減らしてほしいです．
- 気合いを入れましょう．
- 書く時間をもう少し欲しい部分がありました．
  計算はついていけますが，理解が追いついていないので，もう一度ゆっくりレジュメを振り返ろうと思います．
- それが大事だと思います．
- ずっと数学の話だったので，あまり楽しくはなかった．
- そうですか．でも数学が楽しくないと，情報システム工学科での居場所がなくなりますよ．
- この対角化の解法は，すべての形に対して成り立つわけではないのですよね？対角化できないときどうすれば良いのでしょうか？今まで通り解く？
- 講義中に説明しましたが，全ての場合に成り立つ訳じゃないです．具体的な対処法について，講義では説明していませんが，どの本が参考になるのかについては紹介しました．
- 固有値，固有ベクトルの意味がこういう事か…とやっとわかりました．でも，もう少しゆっくり進めてほしいです．
- 理解できたのはすばらしいです．今日の内容は一度はやっているはずなので，スピードは少しぐらい早くても大丈夫ですね．だって理解できた訳だし．
- 何の役に立つかよくわからなかったですが，それらが今の勉強につながって，やっとわかってきたような気がします．何かちょっとうれしいです．
- すばらしい！
- 今日の授業は全部線形でしたね．やはり非線形を学ぶにも線形は大事なのでしょうか？
- もちろんです．必要条件です．
- 線形が非線形を考える為にあるものだという事が，今回の授業でよくわかりました．
- ．．．の為というのがよいかどうかは微妙ですね．
- 対角化や固有値，固有ベクトルの意味を知る事が非線形なものを考えるのになぜ必要なのかがわかりません．なぜでしょう？
- 講義中に何回も言いましたが，局所的に線形で捉えることが出来るからです．
- Pを出し，伸び縮みを出す事によって何をしたいかがわからなくなりました．
- 寝ているからですね．．．
- x(0)=Pとしたのは説明を簡単にする為ですか？収束するしないならば，Pに限定する必要は無いと思います．
- 説明を簡単にするからではなくて，固有ベクトル方向の初期値をとったら，方向が保存されるからです．安定，不安定多様体上を動くことになるので．
- 池田写像のヤコビ行列を求めるにはθ(t)を x(t+1),y(t+1)に代入してから考えるんですか？それとも３×３のヤコビ行列を求めたりするのですか？
- 2X2です．
- カオスはまだですか？？
- 今日の内容は，カオスを理解する為に必要です．
- なんかカオスから離れている気がして寂しいです．
- 離れていないですよ．理解する為には必要です．

7月12日
- 手紙渡しの実験の話では全く知らないひとに手紙を届けるのに，平均で６人で届いたという結果に驚いた．グラフを見ると，多くとも１０人くらいだという事にさらに驚いた．
- 確かに面白い結果だと思います．ただ，この実験を再現できないという主張をする人もいます．
- 六次の隔たりの用な事は何の事象でも起こるのですか？
- 世界が狭いという意味ではYES，どんな場合でも6かというとそうではないです．
- 手紙渡しの実験とハイパーリンクを考えると，６回ほどリンクを辿れば，目的のHPが見つかるという事でしょうか？ HP探すのとっても苦手で．
- ◯WWWの場合は6という数字ではないです． ◯HP探すのが苦手，良いじゃないですか．
- テレビ番組で手紙渡しの実験に似た事（芸能人の同級生を捜す企画）をやっていたのですが，何十人か辿っていました．やらせですか？
- その番組を見たことがないので，なんとも言えないです．その実験では，何トライアルやっていましたか？
- 今度「おうちででかたま」が発売されますよ．息子さんにぜひ．
- 情報をどうもありがとうございます．
- λ_1<1，λ_2<1の時の収束の仕方． λ_2の方が０に近づくスピードが速いので，授業のときに書かれたのとは， λ_2の方向に速く近づくような気がするんですが．
  センターやフォーカスの時，回転の向きが逆だったのですが，発散する時は収束するときの逆回りになるのですか？
- 逆で説明しちゃいましたか？後で確認して，間違っていたら，次回訂正します．
- 「特論」ってなんですか？
- 大学院の講義名でよく使われているようですね．
- ひとの噂が流れる速さは40km/hだと聞いた事があります．
- どうやって測ったかわかりますか？
- 一番最初から今日までのざっとで良いので，まとめや流れの再確認用プリントなどがあるといいです．
- 最終回そうします．
- 固有値が複素数となった時の固有ベクトルの意味は何ですか？
- 講義中に説明しましたが，回転を表します．
- たまごっちがネットワーク機能を本格的に導入した事は今回初めて知りました．六人の隔たりと何か関係があるのでしょうか？
- 僕も最近(半年前くらい)知りました．バンダイのひとがそれを考えていたかどうかは知りません．
- 特性方程式の解のパターンは次数が増えたときも，資料に載っていたパターンのみが存在するのですか？
- 紹介したのは2次元の場合です．
- この世界がネットワークで形成されているとしたら，大きなネットワークの中に複数の小さなネットワークがあって，それらは薄くつながっているという事でしょうか？
- そうですね，そういうイメージでよいのかもしれません．
- 素子の結合の仕方で，ランダムでなく，規則的でない結合の仕方のイメージがわきませんでした．
- 例えば，リングの上に人が並んでいて，各個人は自分の横に並んだ人としかつながっていないような状況です．
- 複雑ネットワークの結合の仕方について，規則的とランダム以外のものがよくわかりません．
- まだ話していないので…．来週話します．
- 今後，非線形の授業は特論まで無いのですか？３年後期や４年とかで．院に行かないと無いのですか？
- 普通無いですね．なので，是非大学院へ進学を！
- 非線形な差分方程式において，３次では３次元的な振る舞いになると予測できるのだけど，それ以上の高次では具体的にどうなるのでしょうか？
- 具体例を挙げている訳じゃないので，具体的には言えないですが．．．
- 池口先生は何か本を出していないのですか？
- 拙著「カオス時系列解析の基礎と応用」産業図書をご覧下さい．

7月19日
- 口頭試問は研究室でするんですか？
- そうです．
- その人が多くのひととつながっていなくても，多くのひととつながりを持つひととつながっていれば，短い経路で多くのひととつながっている事になるので，３人くらいでどの人ともつながっているというのはそこまで不思議な事ではないような気がして．
- そうですね．その通りであると思います．
- この世の中がネットワーク内にも広い世界を持つものがあるのか？
- すみません．質問の意味が分かりにくいです．ネットワーク内の世界というのは，何のことでしょうか．
- 最後の方の規則的でもなくランダムでもない中間というのが納得できませんでした．微妙にランダムでも結局クラスタリングは０になりそうなのですが？
- 規則的でないものは簡単にわかると思います．ランダムネットワークの場合，クラスタリング係数は低く(０)になり，規則的なネットワークの場合，クラスタリング係数は高くなります．また，ランダムネットワークの場合，平均最短経路長は小さくなり，規則的なネットワークの場合，平均最短経路長は長くなります．
  中間というのは，ランダムネットワークのように平均経路長は短いのだが，クラスタリング係数はランダムネットワークのように小さくはならず，むしろ，規則的ネットワークのように大きくなるものです．
- クラスタリング係数の計算がよくわかりませんでした．
- 来週説明しますが，ある人の友達Aとその人の別の友達Bを考えたときに， AとBが友達でもあるという状況をカウントするものです．
- 規則的なグラフの例１での平均次数が2.89になりませんでした．
- おかしいですね．
- 池口先生のErdos数はいくつですか？
- ５です．
- ここでの頂点が「人」のようなものをさす場合，その頂点間の枝を引くための条件は曖昧なものとなってしまうのではないか？
- 確かにそうですね．人でない場合でも，同様の状況があり得ます．
- 講義の内容はある程度理解できたが，実際に何に利用するのかわからなかった．
- 今日の方法論でしょうか．社会的なネットワークでは，なにかあるかもしれないので，調べておきます．
- 現実世界には，規則的なネットワークもランダムなネットワークも探せばありそうな気がしますが，ないんですか？
- 今日御話ししたのは，「ある」ということです．
- 繋ぎ変えるというのがよくわからなかったです．
- いままでのつなぎ先を外して，別のノードに接続する，ということです．
- Random Rewiringによって規則的なネットワークがスモールワールドになるという事をもう少し知りたいと思う．
- 詳しくは，来年でよいでしょう．もちろん，直接質問しにきてくれても構いません．
- 全体のクラスタリング係数も具体例で書いた後，定義式を書いた方がわかりやすかったのでは？
  最近カオスが出てきませんが，来週その関連がわかるのでしょうか？
- ◯具体例はありましたね．
  ◯もちろん関連はあります．
- 規則的なネットワークだと，平均頂点間距離が大きくなる理由がよくわかりませんでした．
- だって，遠くの相手に到達するためには，多数の枝を通らなくちゃ駄目ですよね．
- 完全なランダムネットワークでない現実世界のネットワークでは閉鎖がちな空間の考察も必要なのではないか．
- 「閉鎖しがちな空間」って何でしょうか．
- ６人でアメリカの全国民を網羅できるとしたら， ^6\sqrt{アメリカの国民の数}にクラスタリング係数を何らかの形で作用させる事で，アメリカの国民一人当たりの友人の数の平均を出す事ができるのではないでしょうか？
  Random Rewiringによるスモールワールド化のCとLのグラフですが，元の(p=0)グラフは何を使ったのですか？
- ◯出せると思いますよ． ◯講義中に説明しましたが，一次元状のリングです．
- クラスタリング係数を実際の友人関係に当てはめると…，
  C=1の人：友人ネットワークの中で言えば，いなくても友人関係に変化が無い人（いらない！？）．
  C=0の人：友人間の橋渡し的存在…．
  ウケました．
- 受けてくれたのはよかったですが．．．
- ケーヒニスベルグの橋の問題のような各点間を結ぶ線の数が複数あるようなグラフでは，クラスタリング係数はどのように定義されるのでしょうか？２本を１本と見る？
- よい質問ですね．どのように計算すればよいか，などを考えるだけでも，卒論になると思います．
- 平均頂点間距離やクラスタリング係数の求め方が難しかった．演習の時のグラフよりももっと複雑なグラフになると求め方がかなり面倒くさくなるんじゃないんですか？
- 確かに大変なので，そういうときはコンピュータを用います．
- ピーターセングラフは何かのモデルなのですか？
- かもしれないですね．知らないので，調べておきます．
- グラフと非線形システムのつながりがいまいち良くわかりませんでした．
- √ 各素子は非線形ダイナミクスを有していて，その核素子が，複雑なつながりをしていることを考えたら，面白そうでしょう．
- ネットワークの構造なら，前年度はブラウジングシミュレーションでやりましたが，今日の話で出てきた考え方とは違うものなのでしょうか？
- 総合演習での内容とは違うでしょう．
- グラフ理論について，私は本格的に学んでいないと思うのですが感じているのですが，今回話されたこと以外に重要とされる定理等はありますか？
- 規則的なグラフやランダムグラムについては，従来より多数提案されていると思います．
- 規則があるかないかわからないところに，その規則性を見つけていくのにちょっと面白さを感じた授業でした．
- すばらしい感性ですね．それがわかってくれたら，もう完璧です．
- 現実世界のネットワークはどちらかと言えば「ランダム」に近いと思うのですが，なぜクラスタリング係数が０になってしまうのか．
- ？？？もしランダムだったら，０になるのです．

7月26日　
- 先週に続いてネットワークを学んだが，我々の身の回りに，密接につながっていることが，改めて分かり，研究の必要性が良く分かりました．今回，非線形システムを受講して，紹介のような分かりやすい説明で，この分野に対する興味がわきました．
- 必要性が良く分かってくれたようでよかった．また，興味がわいたという事でよかったです．
- 実験がんばります．
- がんばってください！
- 巡回セールスマン問題の最適解が最適解であることは，全てのパターンを調べなくても言うことができるのでしょうか？
- そういうことです．方法やそのアイディアについては講義中では説明していませんが．
- レポートの内容は決まりました．口頭試問を楽しみにしています．
- 了解．気合いのはいったレポートを期待します．
- 身近な事と大きく関係のあるカオスはやっぱり面白いと思いました．
- その通りです！面白いですよ．
- この「非線形」の分野はまだまだこれからが旬って感じがして池口先生がいつも「おもしろい！！」といっているのもうなづけると思った．
- まだまだ旬です．楽しんでください．
- 全般を通して，カオスや非線形に対する興味が非常に沸きました．ただ，いまだにはっきりと線形と非線形の違いがわかりません．
- あらら，それは困りましたね．．．
- 最後の話を聞いていて思ったのですが，カオスは便利なようだけれども，オーバーテクノロジーな感を受けました．意外と数学の世界の真理なのかも知れませんね．
- 「オーバーテクノロジー」という単語の意味が良く分からないのですが，
  ＃評論家の人がよく使うのしょうかね…
  カオスを応用に使えるはずがない，ということでしょうか．確かに講義では，応用事例について紹介はしませんでしたが，商品化されている例もあります．
- 4ヶ月間ありがとうございました．先生の講義は面白く他の講義と比べても，わかりやすかったです．このような講義の形態は，下手にテストを行なうよりも，理解を深めるのによいと思います．
- わかりやすかったのはよかったです．この調子で，勉強して，来年度はお願いします．
- 今までの講義でその内容の面白さを引出そうとしている先生がいなくて新鮮でした．非線形面白かったです．
- 面白く感じてくれてよかったのですが，過去形にしないで，これからも楽しんでください．
- ハエの個数の話からはじまったこの講義でしたけど，最後にはいろいろな理論の話へと発展していき，社会的なことや生体系のことにもつながるような講義だったので，この講義を学習し終えた上で，もっと非線形に興味を持っていこうと思いました．常にあらゆるところで非線形にふれているのだから，それを普通に流してしまわないようにしたいです．
- すばらしい．その通りです．常に我々は非線形に接しているからこそ，大事なのです．
- ユビキタス社会という言葉の方が身近な気がして非線形がユビキタスというのがいまいち分かりませんでした．レポートの提出期間が長くて助かりました．
- 今のユビキタスというのは，最近日本でも使われだしてきただけで，ユビキタス(ubiquitous)というのは，元々遍在するという意味があります．至る所に有るという意味です．僕も「カオスがユビキタスである」という表現を論文で使ったことがあるぐらいです．もちろん，今のようにユビキタスが使われる以前です．
- 最初は楽しかったですけれど回を重ねるごとに難しくなり理解することが困難になっていきました．でも他の講義とは違って非常に楽しかったです．ありがとうございました．
- そうですか．どの辺りが難しかったでしょうか．その度に質問してくれたらよかったのですが．でも，質問はなかなかしにくいですよね．いずれにしても，楽しんでくれたようでよかったです．
- 脳の情報処理が面白そう
- そうですね．面白いですよ．
- 現在研究中の事，まとめの話等，興味深く聞けました．
- 最後は研究紹介のようになってしまいましたが，興味を持ってもらったようでよかったです．どの辺りに興味を持ちましたか？
- 複雑ネットワークがここまで身近なものだということを知ることができた．非線形というのはここまで幅広い物だというのを知ることができた．
- そうですね，共に身近で様々な場面で出現してきます．なので，大事なのです．
- ここ何回かの複雑ネットワークの講義は分かりやすく最近もいろいろな新しい発見があるのでおもしろかった．自分でもちょっと勉強をしてみたくなりました．ただ英語の本を読むのは苦手なので，途中で諦めるかもしれません．非線形システム概論は，めずらしくおもしろい授業でした．アンケートも"A"ばかりです．
- 「ちょっと」だけなんて言わず，沢山やってください．英語は諦めずに続ければ絶対出来るようになります．アンケートについては，正直嬉しいですが，分かりにくいところもあったと思うので，本当のところを書いてもらって構いません．
- ハイパーリンクの例を聞いて，スケールフリーの話はなるほどと思った．ハイパーリンクで人間がyahooやgoogleの大手にリンクをはるっていうのは人間の心理的な部分も関与しているので心理学の分野でも非線形な解析をしてみるとおもしろいのではないかと思う．
- その通りだと思います．３年生でそういうアイディアが浮かぶのはとてもすばらしい．この調子で進んでください．
- 分野は違っても関連があるというのは，世界の真理に迫っているように感じられて非常に面白い．この講義で，カオスというものが少しは理解できた気がする．
- いや，最初の言葉で，あなたがよく理解できている事が分かります．まさに，世界の真理です．
- 先生の説明は分かりやすくて，話もおもしろかったので，楽しい授業でした．カオスとか非線形とか難しいイメージで近よりがたかったけど，親近感がわきました．先生の非線形に対するあつい想いが伝わってきました☆
- 確かにイメージというのは沸きにくかったかもしれませんが，決して難しいものではなく，むしろ，身近にあるので，一度納得できれば，より強く実感することが出来ると思います．想いが伝わってよかったです．
- 巡回セールスマン問題は，実際の都市には直接行来することが出来ない都市 (離島：港のある都市経由でしか行けない) などもありますが，そのようなことも考慮して解けるのでしょうか．
- よい質問ですね．解けます．講義で示したのは，そのようなことは考慮しない例ですが．
- 半年間おつかれ様でした．ネットワーク面白かったです．途中，因数分解やらテーラ展開やらでてきてくじけそうになったけれど，池口先生のちゃっめけあるしゃべりでなんとか最後まで出れました．
- くじけずに最後まで出来てよかったです．最後のレポートもちゃんと出してください．
- この講義を受ける前は，非線形とは何かということは，何も分からなかったが，この講義を受けて，非線形について少しは理解できて，興味を持てた．
- 興味が持てたのはとてもよかったです．どの辺りが面白かったでしょうか．
- これまでの講義を受けたことによって非線形に対する興味が高まった．
- どの部分が興味が有りますか？
- 非線形を用いた応用がたくさんあるのだと改めて思いました．
- その通りですね．世の中非線形なので，とてもその通りです．
- スモールワールドネットワークが，規則的であることとランダムネットワークの中間であることは証明されているのですか？それとも中間をスモールワールドネットワークと定義したのでしょうか． NP困難問題とも関わりがあるとは思いませんでした．
- 最初の提案者は，中間を定義したという方が正しいと思います．
- テストじゃなくてレポートにしてくれてありがとうございます．レポートがんばります．
- お礼は不要ですが，レポートをちゃんと出してください．
- 取り組んでいる研究課題の内容が，日常生活との結びつきが強いものが多くて分かりやすく，素晴らしいと思いました．本日の講義は，よくまとめられていていい復習になった．単語を見るとぱっと図や言葉が浮かぶようになった．巡回セールスマン問題とかで，実際道の関係等出てきたらどうなるのだろうか．
- 内容がすぐ浮かぶようになるというのは素晴らしいです．来年度は僕の代わりに講義をやってください．是非． TSPについては，実際の道のように考える問題もあります．興味がありますか？
- 複雑ネットワーク理論はとても現実的な問題に応用できるというのはとても興味深かった．全ての授業を通して驚く発見が多く毎回次回の授業に興味がわく，とても楽しい授業でした．
- いろいろと発見できるということては，それだけ洞察力が深いということでとても素晴らしいですね．これからもこの調子で．
- 身近にも多くの非線形な研究課題があるのだなと思いました．
- そうです．この世は非線形なのです．
- 色々なモデルのネットワークの解析があって面白かった
- どのモデルのどの解析が面白かったでしょうか．
- 巡回セールスマン問題のような問題がすばやくとけるようになるなんて，非線形は便利ですね．
- 証明した訳ではないですし，全ての場合という訳でもないので．是非挑戦してください．
- 巡回セールスマンもんだい挑戦してみたのですが全く違っていました．なぜスパコンでも150億年×6の月日がかかるのか，よくわからないんですがなぜですか？
- スパコンの速度を一秒間に何回の演算が処理できるかで定義します．次に，N都市のTSPを全探索しようとすると， (N-1)!/2分の巡回路数になるので，これらを調べるのに．．．と考えると出てきます．僕の過去のサポートページから，情報システム工学入門のページに飛ぶとその話を紹介したスライドが出ています．
- 最近のバイト先での授業での話し方が先生に似てきて困っています！！どうしましょう…．良く「線形」と「非線形」って区別していましたが，世の中は「線形」と「非線形」だけで全て説明できるのでしょうか？
- お，嬉しい事を言ってくれますね．無理せずにそのまま似ていてください．
  さて，肝心の後半についてですが，「線形」と「非線形」ですべてということにはなります．が，多分質問の意味は，「線形」対「非線形」じゃない分類もあるのではないか，ということだと解釈すると，その通りです．良い質問ですね．例えば，これは講義でも紹介したと思いますが，【決定論」対「確率論」というのも，この世の中をどのように捉えようとするのか，という対立概念の一種です．
- 応用面だけを考えると非常に面白く興味を引かれるもおのばかりだった．問題解決の手段の一つとしてネットワーク理論も学んでおきたい気分になりました．
- それは素晴らしい．気分だけじゃなく，是非学んでください．とても大事です．
- 数学的な非線形性が，ネットワークモデルやカオスや，今日説明されたような様々な研究分野に用いられるとは思いませんでした．応用の手法によって様々な解析が可能な点がすごく面白かったです．
- その意味でも数学はとても重要ということになります．
- ハブのような存在が成長していくと，いわゆる「派閥」と呼べるような一つのハブによってまとまる集団が大きくなり，逆に平均頂点間距離が大きくなっていくような状態が出来てしまうような気がしたのですが，どうなのでしょうか．
- 鋭い質問ですね．このような「派閥」が出来るのかちょっとイマイチひらめかないのですが，選択確率を極端な次数依存にするとそうなりそうですね．ただ，スケールフリーネットワークについては，平均頂点間距離は小さくなるはずなんだけど… ちょっと考えてみます．
- 身近にあるものの全ては非線形だと思います．それについて自分なりに考えたいです．
- 本当に考えてくださいね〜．
- 半年間ですごく非線形に興味がひかれました．今日の講義でまだまだ非線形についての研究からなにやら色々あるんだなと思い，この先進む道としてちょっと頭にいれといてもいいかなと思いました．
- そんなそんな，ちょっとと言わずに，是非考えてみましょう．
- 非線形はもう少し狭い分野での話かと思っていたが，様々な例を見て，すごいいろいろなところで使用用途があり，これこそ非線形は，カオス的な広がりがあると思い，興味がよりわいた．
- 非線形の方が線形より，明らかに広い概念なので，その通りだと思います．
- 巡回セールスマン問題の最適解の検証の方法を聞きたかったです．カオスを用いるとNP問題を速く解けるとは驚きです．池田写像のヤコビ行列の解答が示されていない気がするのですがどうでしょうか．
- 検証の方法は，別途チャンスがあればにします．最適性の保証について，興味があれば，参考書籍を紹介します．速く解けるというのは，あくまでも数値実験の結果であって，証明がある訳ではないので，注意してください．池田写像のヤコビ行列，すみません．上げておきました．
- 応用の話を聞くと，面白そうだと思います．が，近似とかその解が正しいか示すのはどうやってやるんだろう？と難しそうな印象が強いです．
- 確かに応用は面白い．でも，基礎的な話もおもしろいですよ．あと，最適性の保証については，興味があれば，参考書籍を紹介します．
- 6次の隔たりに関する文けんを読んでみたいと思った．世実(現実？)世界と関連がある研究は興味深い．
- 紹介しますので，是非読んでみてください．
- 巡回セールスマン問題がなんだか不思議で面白かったです． 24978都市の問題の最適解を実際にどのようにして求めたのか…? と考えると…??? しかもその都市で900億年…？なんでそうなるのかもうーんなんだかよく想像がつきません…
  あっと言う間にこの講義ももうおわりですね．「カオスの中にまだ誰も知らない法測がありそう」という話が印象的でした．本当に誰も知らない事を見つけるのが「研究」なんだな，と実感してなんだかドキドキしました．
- なかなかよい事書いていると思いますが．．．もう少し深く考えるようにするとよいですね．きっと． TSPについては，興味があれば紹介します．
- NP問題の高速計算にカオスが用いられるというのは面白いと思います． DFSで求められるのは相当データ量が少ないですし．全体として直感的に，わかりやすい進め方 (図，実演，自然言語による言いかえ)で，理解が助かりました．
- DFSって何でしょう．

リンク

池口徹担当講義サポートページ
非線形システム概論サポートページ

Email: tohru@ics.saitama-u.ac.jp.